Hiệp phương sai và nghịch đảo là những thuộc tính quan trọng được sử dụng rộng rãi khi xem xét các hàm. Nhiều học sinh đặt câu hỏi Khi nào thì một hàm hiệp biến? Phương pháp xem xét các biến tích cực và tiêu cực là gì? Với bài viết này, Winbet9 sẽ giúp các bạn ôn lại những kiến thức có thể vận dụng vào làm bài tập. Hãy cùng nhau đọc!
Khái niệm hiệp phương sai của hàm số
Cho K là một khoảng, đoạn hoặc nửa khoảng và y = f(x) là một hàm xác định trên K.
Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu:
x1, x2 ∊ K và x1 < x2 thì f (x1) < f (x2)
Đồ thị của hàm số là một đường thẳng đi lên. Hàm đồng biến hoặc nghịch biến trên K còn được gọi là hàm đơn điệu trên K.
Khi nào thì một hàm hiệp biến?
Hàm số f đồng biến trên K khi và chỉ khi:
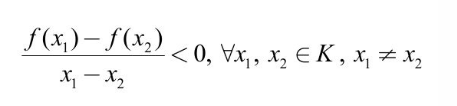
Một điều kiện đủ cho hiệp phương sai của một chức năng
Cho hàm số f có đạo hàm trên K.
Nếu f'(x) > 0 với mọi x ∈ K thì hàm f đồng biến trên K.
Chia sẻ thông tin Cần cù bù cái gì? Cần cù bù thông minh là đúng hay sai?
Phương pháp hạch toán các biến tích cực và tiêu cực
Để xét hàm đồng biến và nghịch biến ta cần áp dụng phương pháp sau:
- Tìm một tập hợp cụ thể
- Tính đạo hàm f'(x). Tìm các điểm xi (i = 1 , 2 ,,…, n) tại đó f'(x) bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và nhập sự thay đổi trong bảng.
- Hình thành kết luận về khoảng đồng biến và nghịch biến của hàm số.
Chẳng hạn, tìm m để hàm số đồng biến trên khoảng
Dạng 1: Tìm m sao cho hàm số đồng biến trên R, nghịch biến trên R.
Dạng toán này thường xảy ra với đa thức bậc 3. Ta có công thức sau:

Ví dụ:
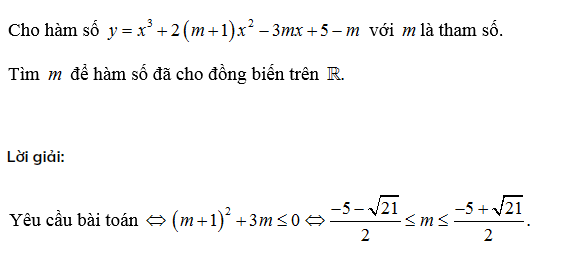
Dạng 2: tìm m sao cho hàm số đồng biến và nghịch biến trên mọi khoảng cho trước.
Dạng này thường xảy ra trong hàm tuyến tính (hoặc hàm phân số bậc 1 trên lũy thừa 1). Ta áp dụng công thức sau:

Ví dụ:

Dạng 3: nhẩm tìm nghiệm của đạo hàm
Ví dụ:
Cho hàm số y u003d x³ – (m+1)x² – (m²-2m)x + 2020. Tìm m để hàm số nghịch biến trên đoạn (0; 1).
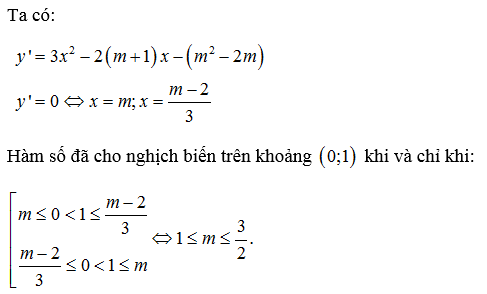
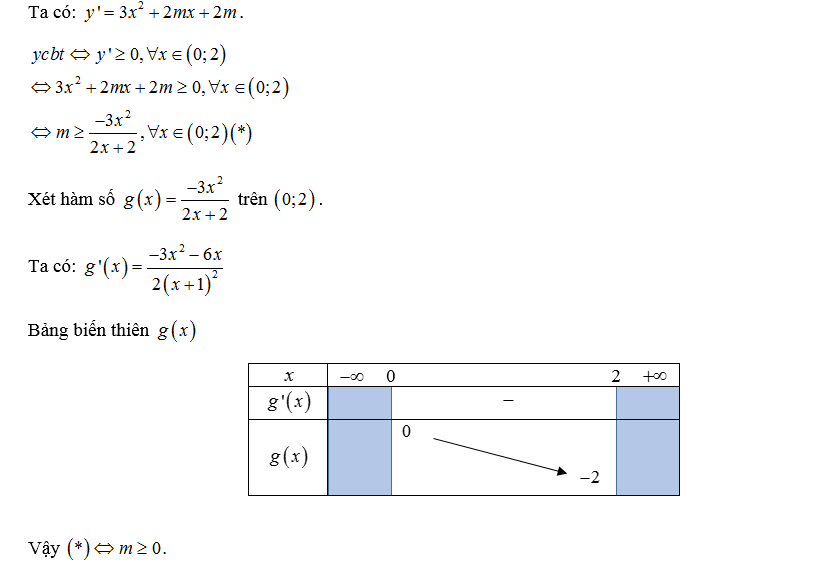
Dạng 4: Cô lập tham số m
Ví dụ:
Cho hàm số y = x³ + mx² + 2mx + 3. Tìm điều kiện m để hàm số đồng biến trên khoảng (0;2).
Câu trả lời:
Dạng 5: Hàm số tuyến tính đơn điệu trên một khoảng cho trước
Nếu đây là một hàm tuyến tính có tham số thì rất có thể xảy ra trường hợp hàm suy biến. Ta cần xét trường hợp hàm suy biến thành hàm bậc nhất.
Trường hợp khác hàm số suy biến thành hằng số thì không cần xét, vì hàm số này không phải là hàm số đơn điệu. Nếu chúng ta xem xét một hàm suy biến, thì chúng ta có thể áp dụng công thức sau:

Ví dụ 1:
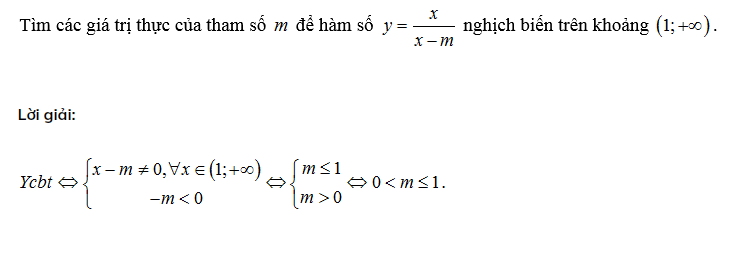
Ví dụ 2:
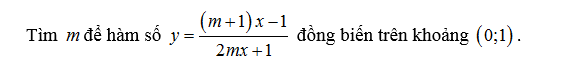
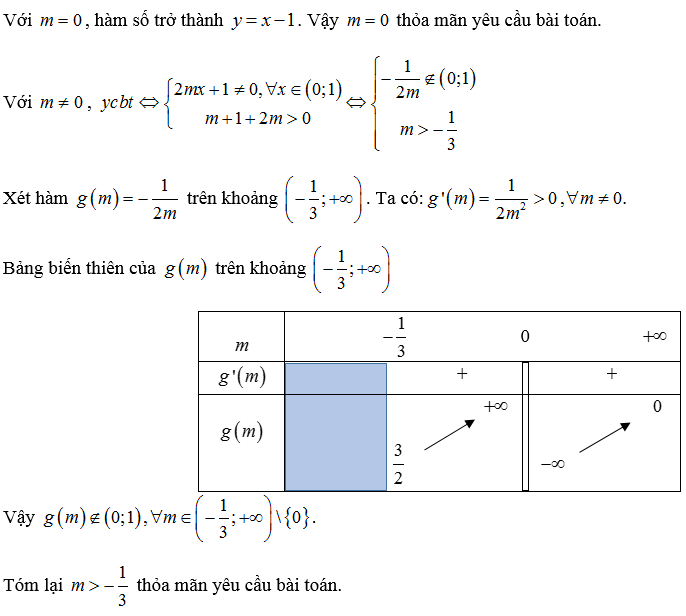
Có thể bạn chưa biết Bài thơ Đôi Dép của tác giả Nguyễn Trung Kiên.
Trên đây là các kiến thức về hàm số đồng biến khi nào, khi nào, phương pháp giải và một số bài toán ví dụ. Hi vọng có thể giúp các bạn củng cố kiến thức và học tốt để làm bài tốt trong kì thi THPT quốc gia. Chúc may mắn!
Chơi game nhà cái Wbet ăn tiền uy tín nhất Việt Nam hiện nay
Trở ra trang chủ nhà cái Winbet


